GAME THEORY: The Ultimate Tool for Strategic Decision-Making
I was introduced to the term Game Theory in 2019 when I read this tweet by Naval Ravikant. It stimulated me to study Game Theory and its utility in making effective decisions in personal and professional life.
Here’s how Wikipedia defines Game Theory:
Game theory is the study of mathematical models of strategic interaction among rational decision-makers. It has applications in all fields of social science, as well as in logic, systems science and, computer science.
The Game theory came to inception due to a mathematician’s interest in poker. John von Neumann, according to a Forbes article “was only interested in poker because he saw it as a path toward developing a Mathematics of Life itself.”
He “wanted a general theory— he called it ‘Game Theory’—that could be applied to diplomacy, war, love, evolution or business strategy.”
In 1944, John Von Neumann teamed up with the economist Oskar Morgenstern to publish the bible of game theory, A Theory of Games and Economic Behavior.
What’s a Game?
A game is a set of circumstances involving two or more decision-makers (players) where each person’s benefit or loss is affected by the decisions of others. So basically, any social interaction is a game, which is why the Game Theory is a mathematical theory of life.
The rules of a game are simple. There are two or more players who make rational decisions to maximize their payoff. Players can be individuals like you and me or big firms like Samsung and Apple.
One of the most famous thought experiments in Game Theory is the Prisoner’s Dilemma. Let us talk about it to have a deeper understanding of this theory.
Prisoner’s Dilemma
The prisoner's dilemma is a standard example of a game analyzed in game theory that shows why two completely rational individuals might not cooperate, even if it appears that it is in their best interests to do so.
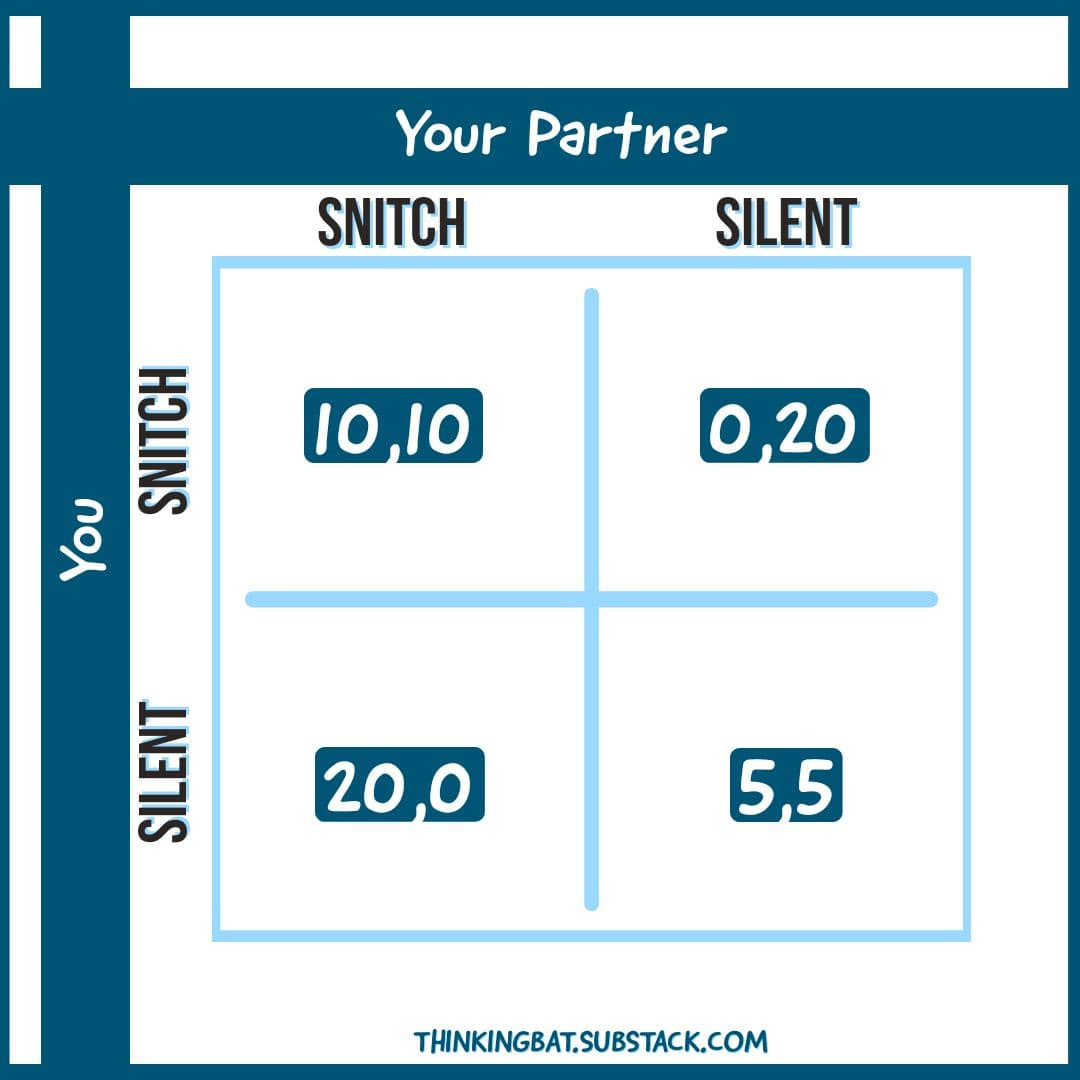
Imagine you with a member of your gang, Robin, get caught red-handed on a crime scene. Both of you are in solitary confinement with no means of communication with each other. The police lack sufficient evidence to convict you for the principal charge, but, they have enough to convict you both for a lesser charge.
For instance, you get caught vandalizing a mansion where the police found a dead body as well. Now the police can convict both of you for vandalism but, they do not have sufficient evidence to arrest you as murders.
Now the inspector in charge of this case puts you in different interrogation rooms and lay out the consequences:
If you snitch on the other person, blaming him for the murder, and the other person does not—you get to walk free.
If you remain silent and your partner snitches—you get 20 years of imprisonment.
If both of you snitch on each other—you both get ten years in prison.
If both of you remain silent— you both get to be in jail for five years.
What would you do? Would you risk staying silent and trust your partner, who is a criminal, to do the same?
Although the ideal condition—the win-win situation— is the one where both of you choose to stay silent, yet the most rational thing to do is to snitch because by doing so, you are trusting a stranger who is also a criminal to stay silent as well when he has a clear opportunity to gain a lot—walk out free.
Nash Equilibrium
The case where you both decide to stay silent is called the Nash Equilibrium.
The Nash equilibrium is a concept of game theory where the optimal outcome of a game is one where no player has an incentive to deviate from his chosen strategy after considering an opponent's choice.
If you observe carefully, you will conclude that staying silent is riskier than snitching—because, considering your unawareness about your partner’s decision, it gives you a chance to either walk free out of this case or to serve the imprisonment of 10 years with your partner, which could have been 20 if you had decided to stay silent.
Dominant Strategy
The case where you both decide to betray each other is called the Dominant Strategy.
In the dominant strategy, each player's best strategy is unaffected by the actions of other players. This renders the critical assumption of the Nash equilibrium—that each actor knows the optimal strategy of the other players—possible but almost pointless.
It would have been a little less risky if you could discuss before making any decision and chose to cooperate by staying silent. This brings me to the next section of this essay—cooperative and non-cooperative games.
Cooperative and Non-cooperative Games
The above-discussed game, prisoner’s dilemma, was an example of a non-cooperative game. You are not aware of your partner’s choices and decisions.
According to Wikipedia, a game is cooperative if the players can form binding commitments externally enforced (e.g. through contract law). A game is non-cooperative if players cannot form alliances or if all agreements need to be self-enforcing (e.g. through credible threats).
Forget the prisoner’s dilemma for a while. Think about the world you live in. It is not like the game of prisoner’s dilemma, where there are constraints preventing you from forming alliances with others. You can collaborate with anyone you want.
This is where Iterated Prisoner’s Dilemma comes to play.
If two players play prisoner's dilemma more than once in succession and they remember previous actions of their opponent and change their strategy accordingly, the game is called iterated prisoner's dilemma.
Now that you can play the game multiple times, one of you may take the risk of cooperation to see if the other person would the same, as it is more beneficial.
There are many versions of the prisoner’s dilemma game that involve financial gains and losses instead of something as dreadful as imprisonment. In those games, it is a little easier to take risks than it is in prisoner’s dilemma.
Watch this video to better understand how the iterated prisoner’s dilemma builds trust and cooperation. I highly recommend you to do so.
Important Decision-Making Lessons to Keep in Mind
Here are the key takeaways from what we have discussed in this essay until now.
Lesson 1: You should never play a strictly dominated strategy if you can cooperate.
Lesson 2: Rational play by rational players can lead to a bad outcome.
Lesson 3: To figure out what actions you should choose in a game, the first step is to figure out what are your payoffs (what do you care about) and what are other players' payoffs.
Lesson 4: If you do not have a dominant strategy, put yourself in your opponents' shoes to try to predict what they will do.
Enough of these complex terms of microeconomics. Let me relax your mental muscles and shed some light on the real-life applications of the game theory.
Real-Life Examples
Game theory is incredibly wide-ranging, and it is used all the time by economists, business strategists, political scientists, biologists, military tacticians, and psychologists. Here are a few situations where the fundamentals of game theory can be applied.
Environmental Studies
It is argued that all countries will benefit from a stable climate, but any single country is often hesitant to curb CO2 emissions.
The immediate benefit to any one country from maintaining current behavior is wrongly perceived to be greater than the purported eventual benefit to that country if all countries' behavior was changed.
Here’s how Game Theory is applicable in Environmental Studies.
Animals
Often animals engage in long-term partnerships, which can be more specifically modeled as iterated prisoner's dilemma. For example, guppies inspect predators cooperatively in groups, and they are thought to punish non-cooperative inspectors.
Due to the tribal nature of their communities, game theory can be used to analyze the behavior of animals.
Psychology
George Ainslie, in his addiction research, points out that addiction can be cast as an intertemporal PD problem between the present and future selves of the addict.
In this case, betrayal means relapsing, and it is easy to see that not betraying both today and in the future is by far the best outcome.
Economics
Oligopolistic competition (when selected firms dominated a market by allying) is a very accurate example of a cooperative game.
Advertising is sometimes cited as a real-example of the prisoner's dilemma. Here is a fascinating Wikipedia section that uses the example of two cigarette companies deciding their advertising budget.
Sport
Doping in sports has been cited as an example of a prisoner's dilemma.
Two competing athletes have the option to use an illegal and/or dangerous drug to boost their performance.
If neither athlete takes the drug, then neither gains an advantage.
If only one does, then that athlete gains a significant advantage over their competitor, reduced by the legal and/or medical dangers of having taken the drug.
If both athletes take the drug, however, the benefits cancel out and only the dangers remain, putting them both in a worse position than if neither had used doping.
Game theory has wide applications, almost every instance of social interaction can be analyzed using Game Theory.
Here’s a clip from A Beautiful Mind where the inception of Nash equilibrium was portrayed exceptionally:
Resources for the Curious Minds
Yale University’s course on Game Theory by Ben Polak. I am halfway through this course and, I’m in love with Ben’s style of teaching, his use of the sense of humor and Socratic questioning to get you engaged as a learner is brilliant.
Wikipedia articles:
Recommended Books:
Reading and studying all of this might be overwhelming for most of you. So, I recommend you to at least start with Yale University’s course on Game theory. Trust me, it’s the best place to study a complex subject like this.
I appreciate your patience and dedication to read this endless essay. If you have any doubts or suggestions please comment below or you can DM me on Twitter.
More than having a large audience, I want a sustainable audience of the right people. People who get something out of these weekly essays. If you know someone who fits the bill, feel free to share my work with them. And if you are new here and like what you have read, then by all means subscribe.
Thank you.